The mean value of a continuous variable

How do we find the mean value of several values?

It seems easy to answer when considering a finite amount of values for which we want the mean value. For example, if we have five values (2,4,5,7,9), we must sum them up and divide them by 5.

But what do we do if we have an infinite number of values? Let’s say that we want to find the mean speed of a car that starts from point A and stops at point B when its speed has been changing arbitrarily during the travel. While the car speeds from 0 m/sec to 1 m/sec, its speed takes all the values between 0 and 1, and this is an infinite number of values. The same happens with a patient’s arterial blood pressure. Pressure does not jump from one value to the next. Although we can only measure the pressure a finite number of times, the pressure takes an infinite number of values as it increases and decreases.

How do we calculate the mean value of an infinite number of values? We cannot add them up and divide them by infinity because infinity is not a number.

Let’s assume that in Figure 1, we see the graph of all the blood pressure values in the aorta over time. At time point x1 the pressure is y1, and at time x2 the pressure is y2. We want to calculate the mean pressure in the aorta between x1 and x2.

Figure 1

Before we do this, let’s do something that looks simpler. Let’s imagine we have a tank full of water, but the tank has only width and height. It does not have depth. So, the tank contains a very thin film of water with no volume but an area. For something to have a volume, it needs to be three-dimensional. On the contrary, an area is two-dimensional. Also, let’s imagine that the film of water in the tank has been left to settle so its surface is horizontal. This hypothetical tank is shown in Figure 2.

Figure 2. The dotted lines represent vertical cross-sections of the tank at various points across its width.

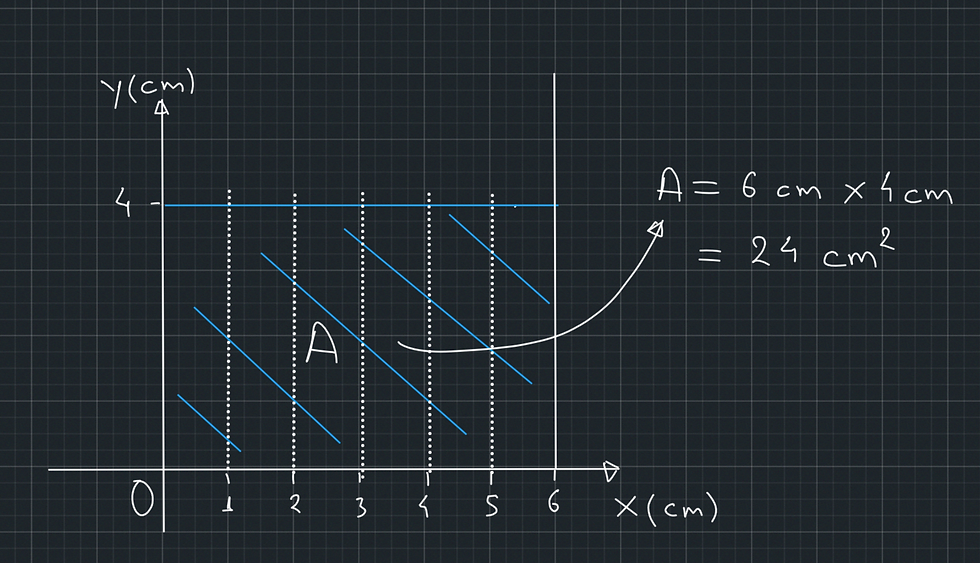
Starting from point O, the width of the water film changes along the x-axis and its height changes along the y-axis. At the vertical cross-section of the tank at width x = 1 cm, the height of the water surface is 4 cm. The water surface has the same height at cross-sections x = 2 cm, x = 3 cm, x = 4 cm, x = 5 cm, x = 6 cm, and at all cross-sections in between. In other words, the water surface in the tank has the same height (x = 4 cm) throughout the width of the tank. This means that the mean value of the height of the water surface is also 4 cm.

Another way to find the mean height of the water surface of this tank would be to divide the area of the tank by its width. The area of the tank is A (cm^2) = Height (cm) x Width (cm). So, if we divide the area A by the Width, we will end up with the Height, which we agreed is the mean value of the height of the surface in this tank.

So, if we were given the surface area A and the width of the tank, we should be able to calculate the mean height of the water surface without knowing the Height of the water surface at any cross-section of the tank.

Although this must seem mind-blowing to most (it was to me when I first encountered this concept), it feels that we have not achieved much yet. But let’s proceed to a different scenario.

Let’s now assume that the same tank with the same amount of water is shaken so that the water surface stops being horizontal and becomes “wavy”. This is illustrated in Figure 3. What is the mean height of the water surface now?

Figure 3

Above, we said that the mean value of the height can be found by dividing the surface of the area by its width. Well, we haven’t added or removed any water from the tank, meaning the water's surface must be the same. The width of the tank is also unchanged.

This means that the mean height of the water surface is still 4 cm!

If we think about it a bit more, we will see that since the total amount of water remains constant, it must be that the area A1, which is the amount of water above the height of 4 cm, equals the area A2, which is where this water must have moved from. Water moved from A2 to A1. So, if the amount of water molecules that moved up is the same as the amount of water molecules that moved down, it must be that the mean height of the surface is unchanged.

If you are still unconvinced, imagine we have three values (6,4,5), and their mean is 5. What will happen to the mean if one value increases by 2 and another decreases by 2? The sum of all three values will remain unchanged. To find their mean, we must divide their sum by 3, giving us the same mean value of 5.

It can be shown using formal mathematics that the mean value of any continuous quantity illustrated as a line (straight or curved) is the area underneath the line divided by the width of the area. We don’t care what this formal proof looks like because we are not studying theoretical mathematics. We do applied mathematics and all we need to know is that this has been proven, and we can use it in any application we need to find the mean value of a continuous quantity.

So, what does that have to do with mechanics in orthopaedics?

One of the many applications is the stress and energy a material absorbs when loaded. If we wanted to be accurate, instead of saying “stress”, we should say “mean stress”. But because we know we mean the mean stress, we just call it “stress”. As we will see in other posts, realising that we are talking about the mean stress of the different stresses along the cross-section of a beam and understanding what the mean is will help us understand mechanics better. There is only one thing that remains to be discussed.

How do we calculate the area under a line in a graph?

We do this by using a technique called “integration”, symbolised by:

So, if the graph in Figure 4 represents a function f(x). Then, the area under the curve between x1 and x2 is symbolised as:

Figure 4

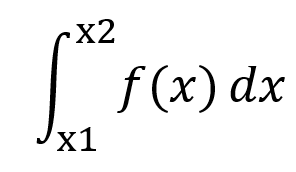
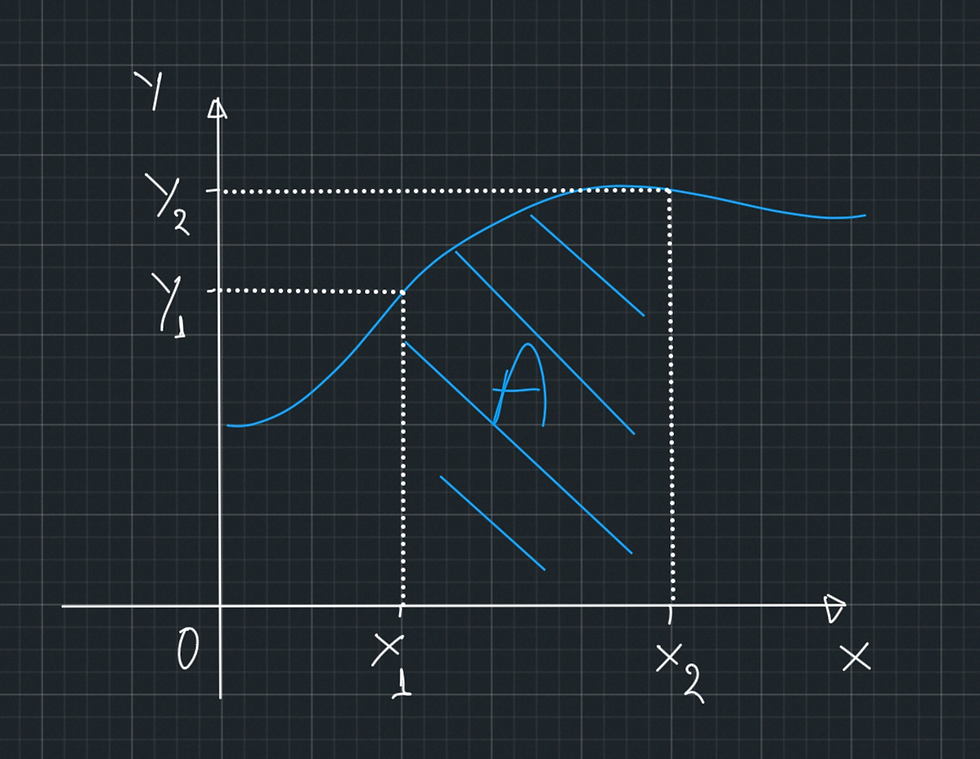
Vice versa, if you ever see the above in a text and you want to translate it into English, then this is translated as “the area under the line of function f(x) between x1 and x2”.

So, if the mean value is the area under the curve divided by the width of the area and the width of the area is x2-x1, then the mean is:

So, if you ever see the above script, you know what it means in English. It is the mean value of all the values this function takes between x1 and x2. If the function f(x) is the blood pressure in the aorta as a function of time, then the above describes the mean blood pressure between time x1 and time x2 in mathematical terms.

I hope the above has helped one understand the mean value of a continuous quantity and how we calculate it.