How to calculate the rotation of the tibial plateau manually

Although most of the times we use charts which will show how much we need to move the proximal tibial fragment to achieve a tibial plateau angle (TPA) of 5o, many times we want to rotate more than that and we don't have access to the charts.

More importantly, we may want to know through what angle the TPA will rotate if we move the proximal fragment a specific distance, say 1 mm.

Below is the trigonometry and the formulas you must remember to manually calculate rotation.

Let's assume that we want to rotate the circle of the figure about its centre C so that we move point A to point B. We know that we want to rotate through an angle θ and we want to calculate the chord d. The chord is what we measure in theatre by marking points A and B either with a cautery or with an osteotome.

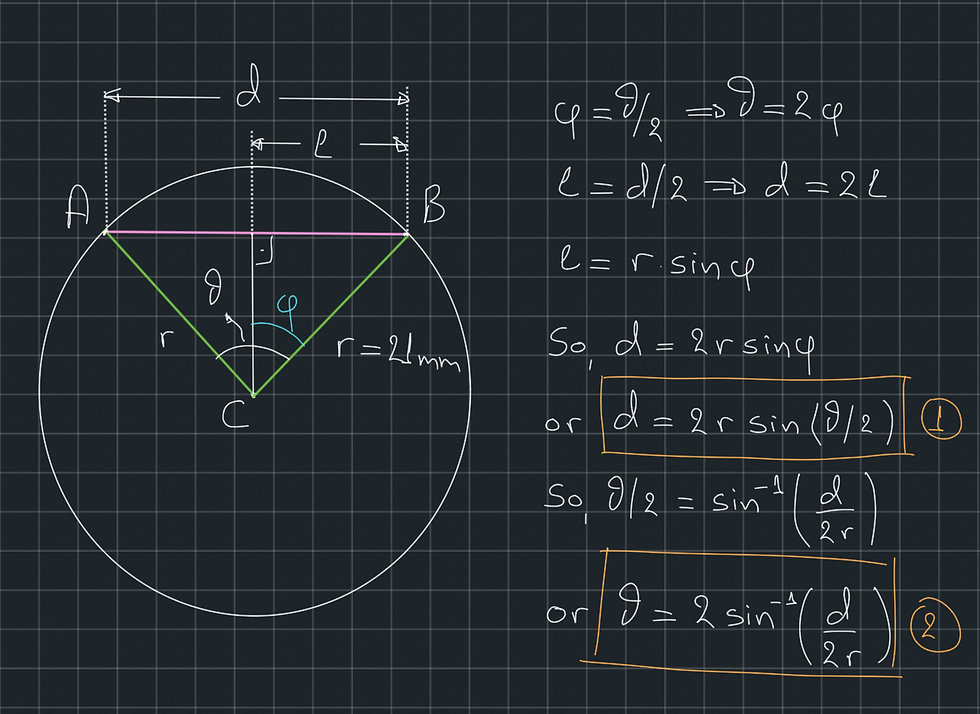
The triangle formed by the two green lines and the pink line is isosceles as the green lines, being the radius of the circle, are equal in length. If we draw a line from the centre of the circle C perpendicular to the pink line, this line will divide the pink side of the triangle (base) into two equal parts. This is a theorem and we don't need to prove it. The theorem states that the altitude (height) to the base of an isosceles triangle bisects the base and the vertex angle. As a reminder, the triangle's height is perpendicular to its base. According to this theorem, angle φ is half of angle θ (vertex angle). Now, we know enough to calculate length l. As l is half of d, we can also calculate d.

So, if we know the radius r of our blade and the angle of intended rotation θ, we can calculate the length of the chord d between points A and B (Equation 1).

What if we know the chord by which we want to rotate and we want to calculate what the angle of rotation θ will be?

All we need to do is solve equation 1 for θ. As a reminder, if we know the sine of an angle, we can find the angle by putting the value of its sine into the function InverseSine, which is written as sin^-1 in the calculators. So, if sinθ = 0.5, then θ = sin^-1(0.5).

The angle through which the TPA rotates by moving A through d can be found using equation 2. If d = 1 mm, then you can calculate through what angle the TPA will rotate by moving A through a chord of 1 mm. This way you can keep moving A through 1 mm increments until you have reached the TPA you wish. You know that every time you move through 1 mm, you rotate the TPA by θ.

The videos below show how you can use your calculator to apply formula 1 and 2.

How to use the calculator to find the chord of rotation if you know the angle of rotation. In this video we use a 21 mm blade and we want to calculate the chord of rotation to rotate the tibial plateau through 20 degrees. Turn the subtitles on for narration.

This is how to calculate through what angle the tibial plateau rotates when the proximal fragment is rotated through 1 mm.