Joint contact reaction force - Part 2 - The intact stifle joint.

In the previous post, we became familiar with finding the reaction elements from a wall when a beam is fixed on it. We said that the wall must apply a force equal in magnitude and opposite in direction to the one we apply to the beam and a moment equal in magnitude and opposite in direction to the one our force will generate.

Although we understand how a fixed-type support reacts, the stifle joint is more of a hinge-type support as it allows the tibia to rotate about the femur. So, let's dig into this type of support using our familiar beam from the previous post.

In Figure 1, the beam is connected to a hinge. If we apply a force FA to the beam, the latter will rotate about the hinge, but it will not translate relative to the hinge. The fact that the beam will not translate means that the hinge will react to our force with a force of the same magnitude and opposite direction. The fact that the beam will rotate means that the hinge will not generate a moment to "resist" the moment that our force will generate.

Figure 1. The green mark represents the hinge-type support (joint). The unknowns are circled in red. There are two equations (hinge reaction force) in two unknowns.

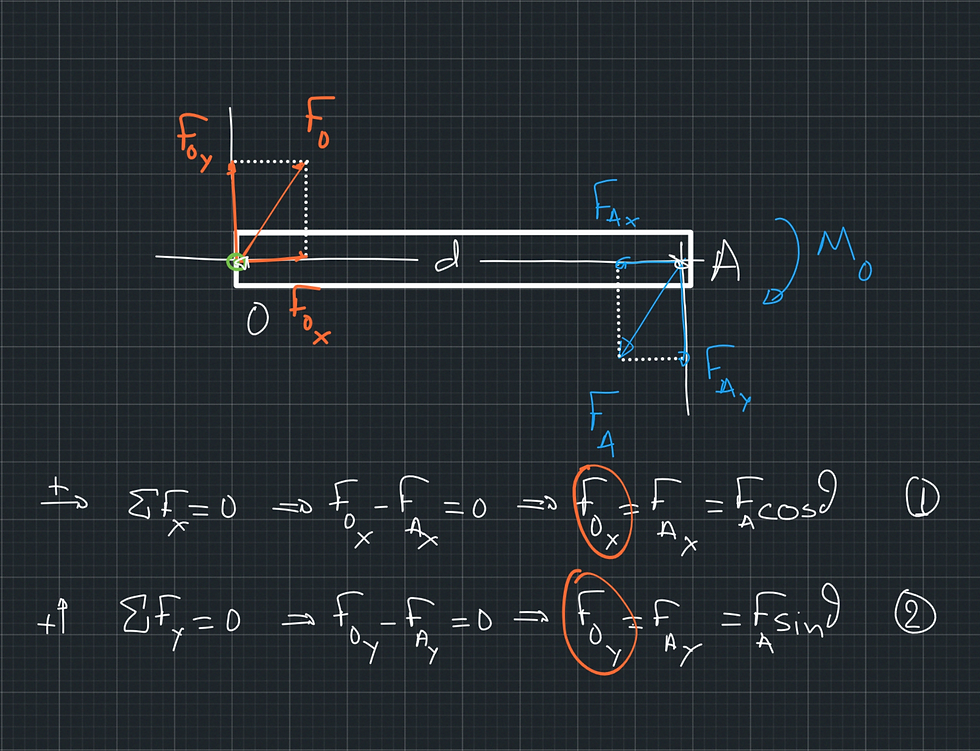
Back to the stifle joint, the hinge is provided by the cranial and caudal cruciate ligaments. These ligaments will react to the tibia's tendency to translate relative to the femur but will not react to its tendency to rotate about the femur. Let's look at the cruciate ligaments as an extension of the femur. We can say that the femur will react to the tibial's force through the cruciate ligaments, with a force of the same magnitude and opposite direction to the one applied to the tibia by the ground and the muscles (FT).

This force is the joint contact reaction force in an intact stifle joint!

If we wanted to analyse the reaction of the hinge to our force FA, we could again follow the same methodology we followed for the fixed-type support (Figure 1). The only difference is that this time, the reaction is only composed of a force. The joint does not apply a moment to resist our force's moment.

The calculation of this force is shown in Figure 1. A similar calculation can be applied in the stifle joint if one knows the magnitude and direction of force FT (Figure 2). As we only have two forces, we don't have to analyse them into orthogonal components. We know that the reaction force would be of the same magnitude and opposite to the action force. If we know the action force FT, then we know the reaction force JRF. But if we wanted to analyse the forces into components, I would choose one of the axes to be the tibial plateau. That is just because I know that if the cruciate ligaments were not there, the tibia would tend to slip on the plateau. But you could choose any axes you wanted. We will look into the choice of the axes in the next post.

Figure 2. Calculation of the joint's reaction force JRF.

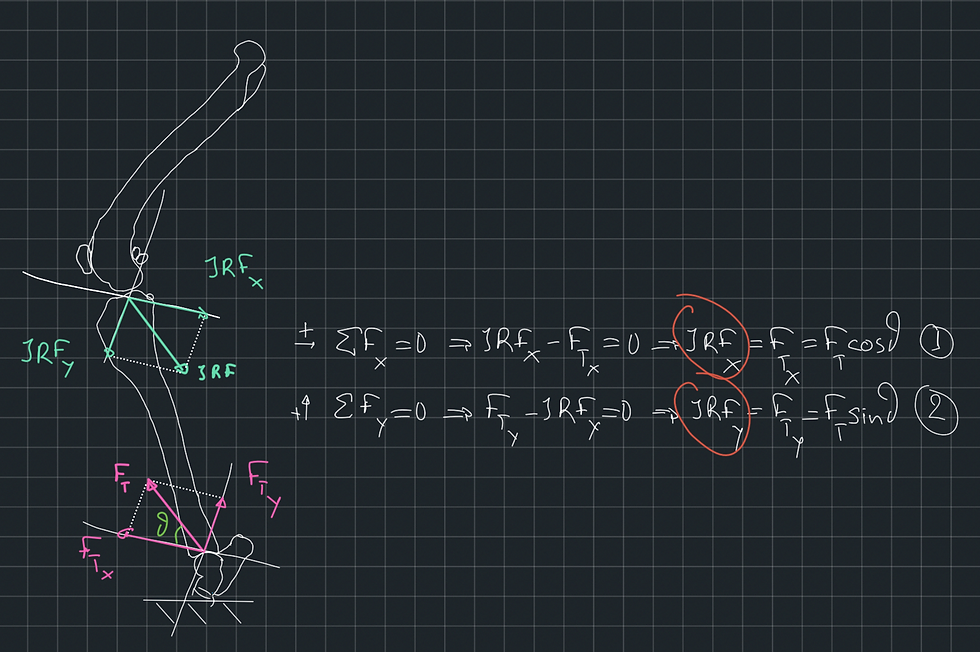
Is that it, then? Is it that easy to calculate the joint contact reaction force? Unfortunately, not. Our simplified idealised models can help us understand what a joint reaction force is. One of the next posts will briefly explain the main factors that bring enormous complexity when we try to calculate the joint contract reaction force in real life.